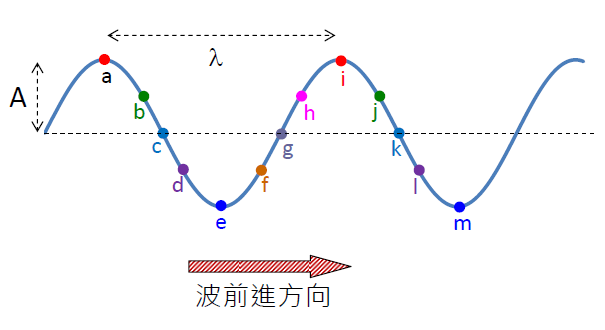
|
|
- 在上圖，波形向右前進，但粒子只作上、下振動。
- 波形不斷重複，波長 (λ) 是波形重複的最短距離， 即是圖中粒子 a 和粒子 i 的距離，也可以是 b 和 j 的距離，....等
- 粒子振動的頻率相同，振幅也相同。但它們之間作存在 相 角 差 。
- 相距一個整波長的粒子是同相關係，例如 a 和 i、 c 和 k、... 等
- 相距半個整波長的粒子是反相關係，即是速度保持相反，例如 a 和 e、 b 和 f、 g 和 k、...等
- 當粒子到達最高點 (波峰) 或最低點 (波谷) 時， 它們的速度為零，稱為瞬時靜止。 而它們經過中間的平衡位置時，速率則最高。
- 以下方法可找出除位於波峰和波谷的粒子外，其餘粒子的行走方向。方法就是在原圖加上很短時間後的新波形。比較這兩新、舊波形，就可推算出每粒粒子現正行走的方向 (不要忘記，粒子只作上、下移動)。
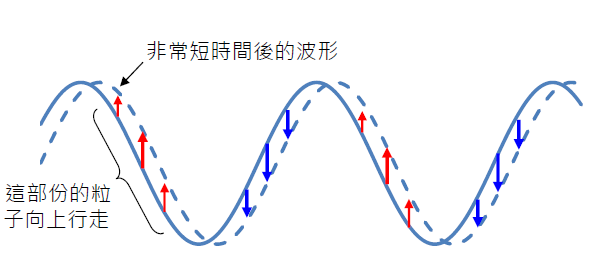
- 如此，我們就可以推算出各粒子自己的位移如何隨時間變化。
假設在上面，有標示粒子的波形是在 t = 0 s 的記錄，那粒子 g 的位移 — 時間線圖應該就是這樣：
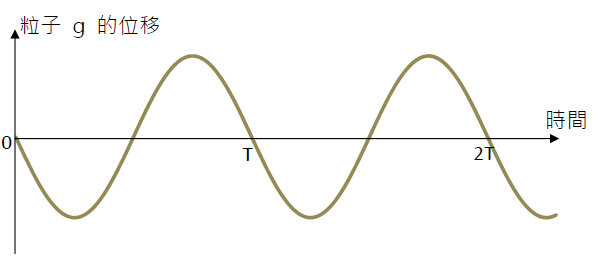上圖的橫軸是時間，所以兩峰之間的「距離」不是波長，而是週期 T (週期是完成一次振動所需時間).
- 在時間 T，波動前進了距離 λ，所以 波速 v = 距 離 ÷ 時 間 = λ / T = f λ，其中 f 是波動頻率 ( 頻率是 1 秒內完成的振動次數。 f 和 T 是倒數關係： f = 1 / T ).
|
|
