|
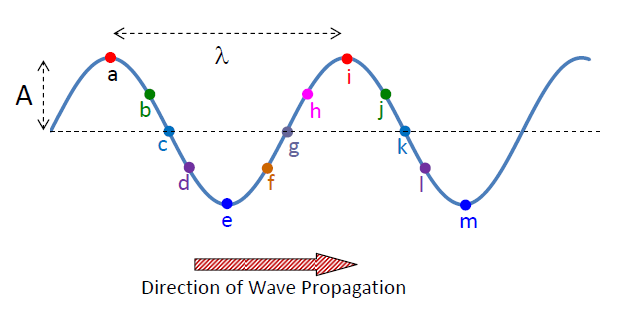
|
- In the figure, the particles vibrate up and down while the waveform moves to the right.
- The minimum distance that the waveform repeats itself is called wavelength (λ), i.e., the distance between the two particles a and i, b and j, or c and k,….
- The particles vibrate at the same frequency, same amplitude but there are phase differences among them.
- Particles separated by a whole wavelength are vibrating in-phase, e.g, particles a and i, c and k,...
- Particles separated by a half wavelength are vibrating exactly out of phase (antiphase), meaning they are always moving in the opposite directions, e.g., particles a and e, b and f, g and k,...
- A particle will be momentarily at rest when it goes up to the highest point (crest) or down to the lowest point (trough), and it will cross the equilibrium line with the fastest speed.
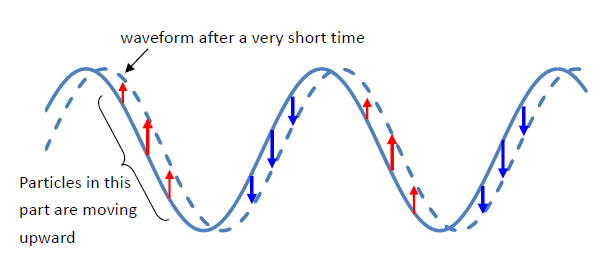
- The directions of movement of particles other than those at the crests and troughs can be found by translating the waveform by a very short distance in the direction of its propagation.
By comparing the two waveforms separated by a very short time interval, we can deduce in what directions the particles are moving (don't forget, they are only moving up and down).
- From the waveform which shows the positions of various particles at an instant, say, t = 0s, we can deduce the displacemt-time graphs of individual particles.
That of particle g labeled in our figure would be plotted like this:
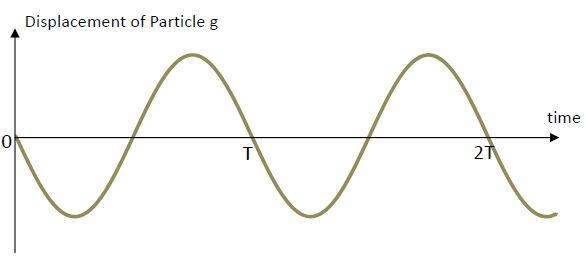 Here, the horizontal axis is time, so the "distance" between two adjacent peaks is not wavelength, it is period T (Period is the time to complete one oscillation).
Here, the horizontal axis is time, so the "distance" between two adjacent peaks is not wavelength, it is period T (Period is the time to complete one oscillation).
- In a time T, the wave advances by a distance λ, so wave speed v = distance / time = λ / T = f λ, where f is the wave frequency ( frquency is the number of oscillations completed in 1 s; f = 1/T ).
|
|