Java Physics

 

RFR

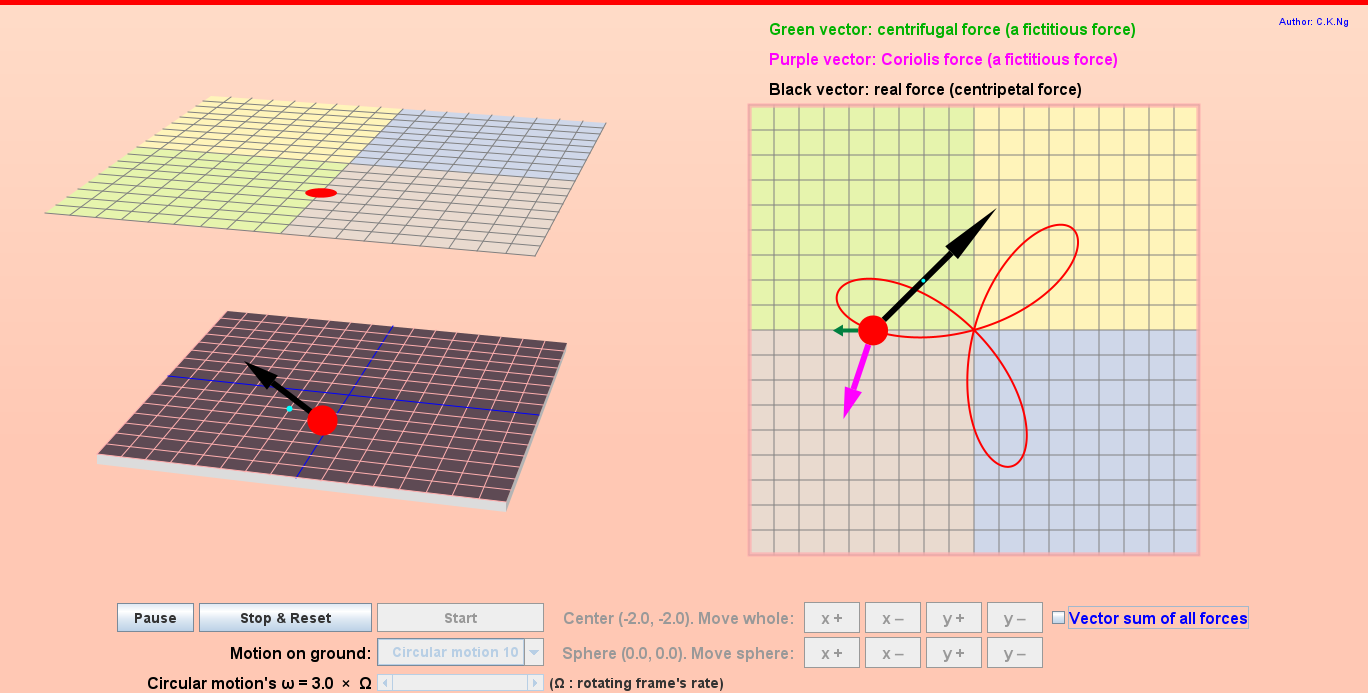
Rotating Frames of Reference (Coriolis and Centrifugal force)

 

 

Reference :

Simple quantitative examples illustrating how the centrifugal and Coriolis forces
"rescue" Newton's second law in rotating frames
(Physics Education, May 2024) Download from PE (Open Access)

Download Executable Jar File

 

 

 

  • The author (Chiu-king Ng) has the copyright on all the simulations in this website.
  • Email phyAA@phy.hk, where AA is the prime number following 7.
  • Last Update:2024-3-8