Internal Links :

Generating Stationary Waves on String

RLC Series Resonance

RLC Parallel Resonance

Download Executable Jar File

Html5 Version

Natural frequency (or called Characteristic Frequency)

That is the frequency at which a system would oscillate by itself if displaced. The natural frequency of a spring-mass system is f_o= √(k/m)/2π, where k is the spring constant and m is the mass of the object attached to the spring.

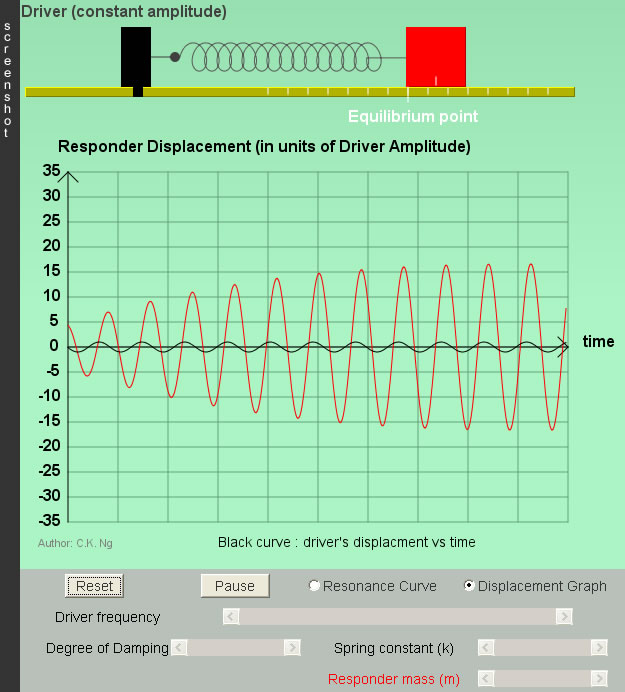
Forced oscillation

A periodic force at a given frequency (called driving frequency f_d) is applied to an oscillating system of natural frequency f_o. At the beginning (transient stage), there is a mixture of two kinds of oscillations, one has the frequency f_o and the other has f_d. The former will gradually die out because of the damping effect. Eventually (at the steady state) the system settles down with oscillation at the frequency of the driving force (f_d).

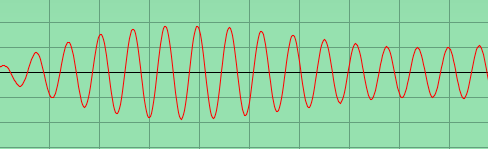
At the transient stage, the object responds to two oscillations (f_o and f_d), the superposition of them forms a BEAT.

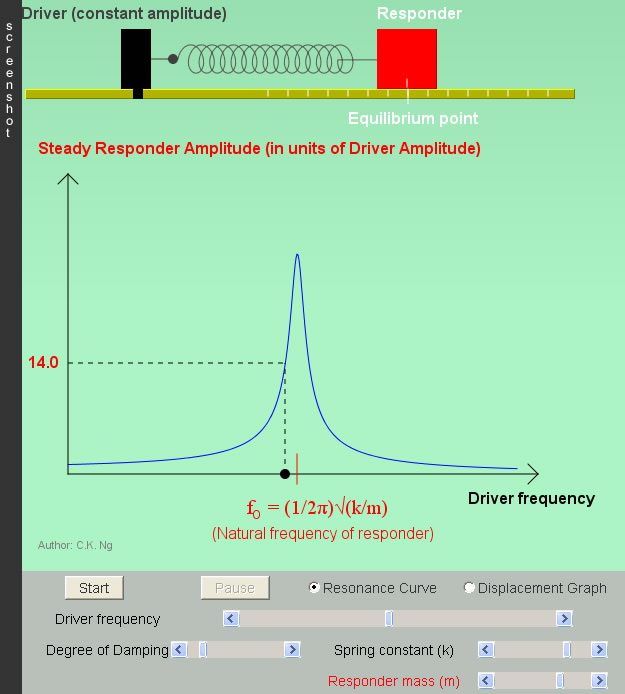
Resonance

When the driving frequency is at the same frequency as the natural frequency of the oscillator, the amplitude of oscillation is at its greatest. When this happens the energy of the oscillator becomes a maximum.

Phase

When f_d << f_o, the responder is in phase with the driver.
When f_d = f_o, the responder lags the driver by 90⁰.
When f_d >> f_o, the responder and the driver are in antiphase.